Background |
Enter Data |
Analyze Data |
Interpret Data |
Report Data
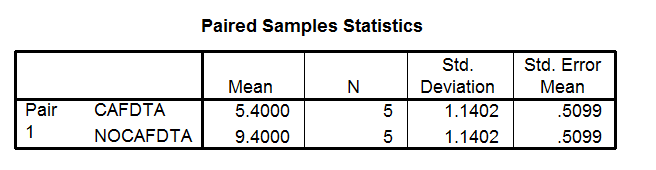
Look at the Paired Samples Statistics Box
Take a look at this box. You can see each variable name in left most column. If you have given your variables meaningful names, you should know exactly which conditions these variable names represent. You can find out the number of participants, mean and standard deviation for each condition by reading across each of the two condition rows.
Example
In the Paired Samples Statistics Box, the mean for the caffeine condition (CAFDTA) is 5.40. The mean for the no caffeine condition (NOCAFDTA) is 9.40. The standard deviation for the caffeine condition is 1.14 and for the no caffeine condition, also 1.14. The number of participants in each condition (N) is 5.
Paired Samples Test Box
This is the next box you will look at. It contains info about the paired samples t-test that you conducted. You will be most interested in the value that is in the final column of this table. Take a look at the Sig. (2-tailed) value.
Sig (2-Tailed) value
This value will tell you if the two condition Means are statistically different. Often times, this value will be referred to as the p value. In this example, the Sig (2-Tailed) value is 0.005.
If the Sig (2-Tailed) value is greater than 05…
You can conclude that there is no statistically significant difference between your two conditions. You can conclude that the differences between condition Means are likely due to chance and not likely due to the IV manipulation.
If the Sig (2-Tailed) value is less than or equal to .05…
You can conclude that there is a statistically significant difference between your two conditions. You can conclude that the differences between condition Means are not likely due to change and are probably due to the IV manipulation. Our ExampleThe Sig. (2-Tailed) value in our example is 0.005. This value is less than .05. Because of this, we can conclude that there is a statistically significant difference between the mean hours of sleep for the caffeine and no caffeine conditions. Since our Paired Samples Statistics box revealed that the Mean number of hours slept for the no caffeine condition was greater than the Mean for the caffeine condition, we can conclude that participants in the no caffeine condition were able to sleep significantly more hours than participants in the caffeine condition.
|
